Effectsize objects

The auxiliary classes involved in the computations of bootstrapped effect sizes.

---

TwoGroupsEffectSize

def TwoGroupsEffectSize(
    control, test, effect_size, proportional:bool=False, is_paired:NoneType=None, ci:int=95, resamples:int=5000,
    permutation_count:int=5000, random_seed:int=12345, ps_adjust:bool=False
):

A class to compute and store the results of bootstrapped mean differences between two groups.

Compute the effect size between two groups.

Example

random.seed(12345)
control = norm.rvs(loc=0, size=30)
test = norm.rvs(loc=0.5, size=30)
effsize = dabest.TwoGroupsEffectSize(control, test, "mean_diff")
effsize

The unpaired mean difference is -0.253 [95%CI -0.782, 0.241].
The p-value of the two-sided permutation t-test is 0.348, calculated for legacy purposes only. 

5000 bootstrap samples were taken; the confidence interval is bias-corrected and accelerated.
Any p-value reported is the probability of observing theeffect size (or greater),
assuming the null hypothesis of zero difference is true.
For each p-value, 5000 reshuffles of the control and test labels were performed.

effsize.to_dict()

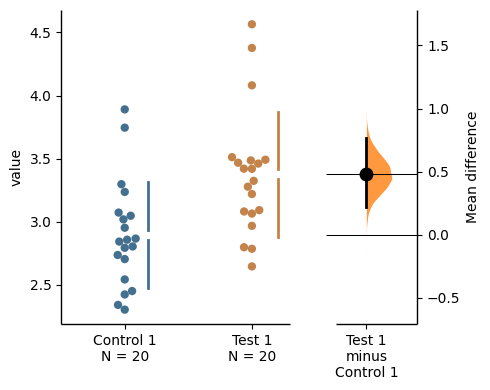
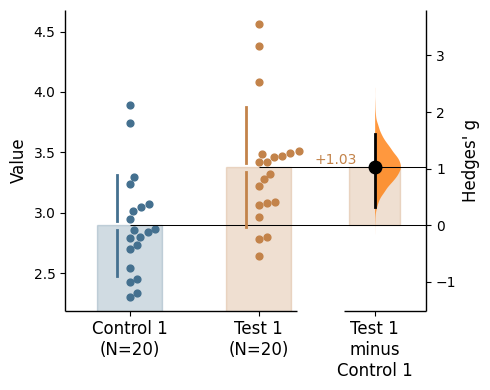
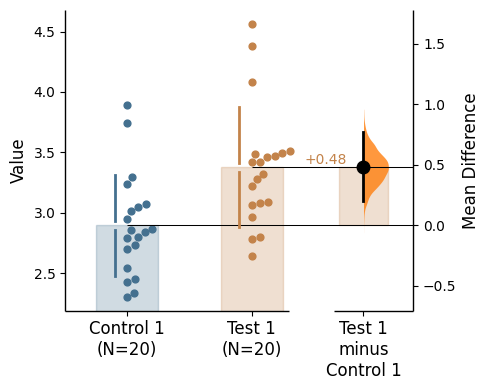
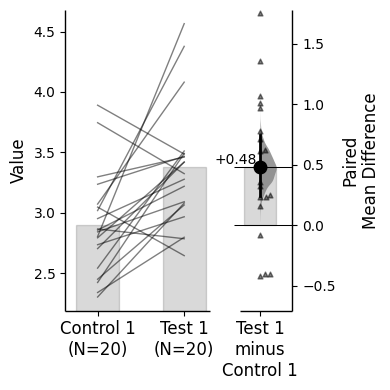
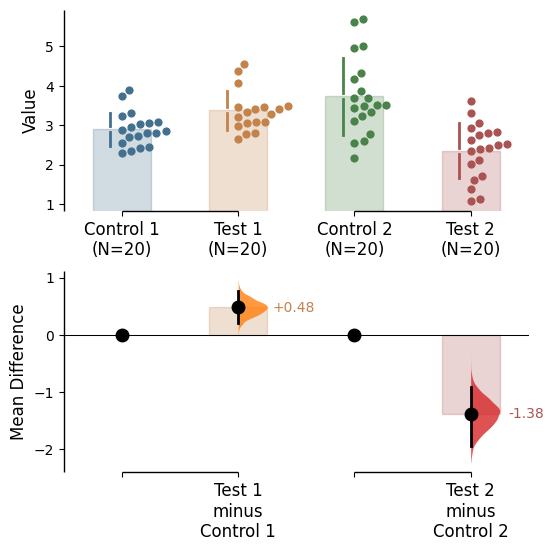
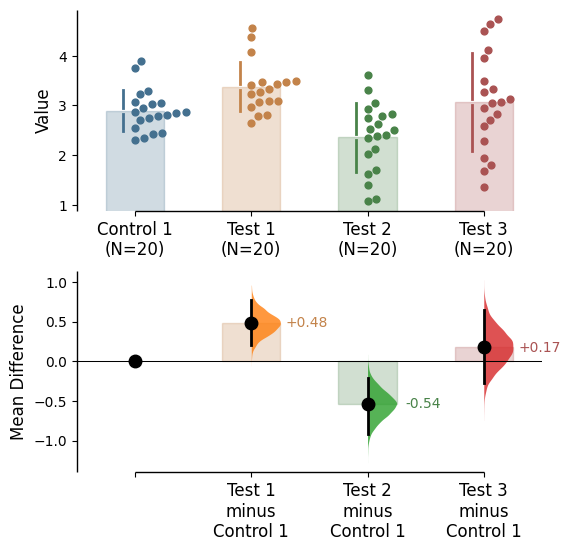
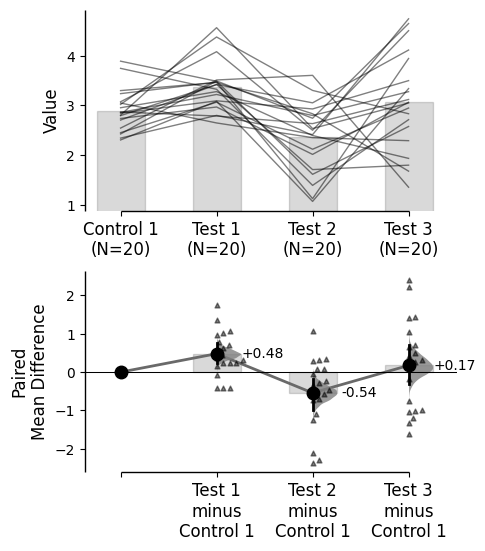
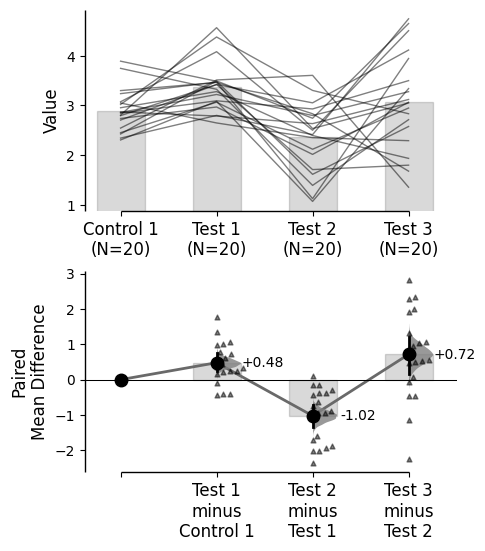
{'alpha': 0.05,
 'bca_high': 0.2413346581369784,
 'bca_interval_idx': (109, 4858),
 'bca_low': -0.7818088458343655,
 'bec_bca_high': 0.5352403905584314,
 'bec_bca_interval_idx': (130, 4880),
 'bec_bca_low': -0.4982839949134528,
 'bec_bootstraps': array([-0.48953946, -0.18565285, -0.23896785, ..., -0.55130928,
         0.16037238, -0.07364879]),
 'bec_difference': 0.0,
 'bec_pct_high': 0.5280564736117328,
 'bec_pct_interval_idx': (125, 4875),
 'bec_pct_low': -0.5041777340626885,
 'bootstraps': array([-0.23923425, -0.66013733, -0.42672232, ..., -0.33191074,
        -0.16543251, -0.34179536]),
 'ci': 95,
 'difference': -0.25315417702752846,
 'effect_size': 'mean difference',
 'is_paired': None,
 'is_proportional': False,
 'pct_high': 0.25135646125431527,
 'pct_interval_idx': (125, 4875),
 'pct_low': -0.763588353717278,
 'permutation_count': 5000,
 'permutations': array([ 0.17221029,  0.03112419, -0.13911387, ..., -0.38007941,
         0.30261507, -0.09073054]),
 'permutations_var': array([0.07201642, 0.07251104, 0.07219407, ..., 0.07003705, 0.07094885,
        0.07238581]),
 'proportional_difference': nan,
 'pvalue_brunner_munzel': nan,
 'pvalue_kruskal': nan,
 'pvalue_mann_whitney': 0.5201446121616038,
 'pvalue_mcnemar': nan,
 'pvalue_paired_students_t': nan,
 'pvalue_permutation': 0.3484,
 'pvalue_students_t': 0.34743913903372836,
 'pvalue_welch': 0.3474493875548964,
 'pvalue_wilcoxon': nan,
 'random_seed': 12345,
 'resamples': 5000,
 'statistic_brunner_munzel': nan,
 'statistic_kruskal': nan,
 'statistic_mann_whitney': 494.0,
 'statistic_mcnemar': nan,
 'statistic_paired_students_t': nan,
 'statistic_students_t': 0.9472545159069105,
 'statistic_welch': 0.9472545159069105,
 'statistic_wilcoxon': nan}

---

EffectSizeDataFrame

def EffectSizeDataFrame(
    dabest, effect_size, is_paired, ci:int=95, proportional:bool=False, resamples:int=5000,
    permutation_count:int=5000, random_seed:int=12345, x1_level:NoneType=None, x2:NoneType=None, delta2:bool=False,
    experiment_label:NoneType=None, mini_meta:bool=False, ps_adjust:bool=False
):

A class that generates and stores the results of bootstrapped effect sizes for several comparisons.

Example: plot

Create a Gardner-Altman estimation plot for the mean difference.

random.seed(9999) # Fix the seed so the results are replicable.
# pop_size = 10000 # Size of each population.
Ns = 20 # The number of samples taken from each population

# Create samples
c1 = norm.rvs(loc=3, scale=0.4, size=Ns)
c2 = norm.rvs(loc=3.5, scale=0.75, size=Ns)
c3 = norm.rvs(loc=3.25, scale=0.4, size=Ns)

t1 = norm.rvs(loc=3.5, scale=0.5, size=Ns)
t2 = norm.rvs(loc=2.5, scale=0.6, size=Ns)
t3 = norm.rvs(loc=3, scale=0.75, size=Ns)
t4 = norm.rvs(loc=3.5, scale=0.75, size=Ns)
t5 = norm.rvs(loc=3.25, scale=0.4, size=Ns)
t6 = norm.rvs(loc=3.25, scale=0.4, size=Ns)


# Add a `gender` column for coloring the data.
females = repeat('Female', Ns/2).tolist()
males = repeat('Male', Ns/2).tolist()
gender = females + males

# Add an `id` column for paired data plotting.
id_col = pd.Series(range(1, Ns+1))

# Combine samples and gender into a DataFrame.
df = pd.DataFrame({'Control 1' : c1,     'Test 1' : t1,
                 'Control 2' : c2,     'Test 2' : t2,
                 'Control 3' : c3,     'Test 3' : t3,
                 'Test 4'    : t4,     'Test 5' : t5, 'Test 6' : t6,
                 'Gender'    : gender, 'ID'  : id_col
                })
my_data = dabest.load(df, idx=("Control 1", "Test 1"))

fig1 = my_data.mean_diff.plot();

Create a Gardner-Altman plot for the Hedges’ g effect size.

fig2 = my_data.hedges_g.plot();

Create a Cumming estimation plot for the mean difference.

fig3 = my_data.mean_diff.plot(float_contrast=True);

Create a paired Gardner-Altman plot.

my_data_paired = dabest.load(df, idx=("Control 1", "Test 1"),
                       id_col = "ID", paired='baseline')
fig4 = my_data_paired.mean_diff.plot();

Create a multi-group Cumming plot.

my_multi_groups = dabest.load(df, id_col = "ID", 
                             idx=(("Control 1", "Test 1"),
                                 ("Control 2", "Test 2")))
fig5 = my_multi_groups.mean_diff.plot();

/Users/jonathananns/GitHub/DABEST-python/dabest/plot_tools.py:2778: UserWarning: 5.0% of the points cannot be placed. You might want to decrease the size of the markers.
  warnings.warn(err)
/Users/jonathananns/GitHub/DABEST-python/dabest/plot_tools.py:2778: UserWarning: 10.0% of the points cannot be placed. You might want to decrease the size of the markers.
  warnings.warn(err)

Create a shared control Cumming plot.

my_shared_control = dabest.load(df, id_col = "ID",
                                 idx=("Control 1", "Test 1",
                                          "Test 2", "Test 3"))
fig6 = my_shared_control.mean_diff.plot();

/Users/jonathananns/GitHub/DABEST-python/dabest/plot_tools.py:2778: UserWarning: 10.0% of the points cannot be placed. You might want to decrease the size of the markers.
  warnings.warn(err)

Create a repeated meausures (against baseline) Slopeplot.

my_rm_baseline = dabest.load(df, id_col = "ID", paired = "baseline",
                                 idx=("Control 1", "Test 1",
                                          "Test 2", "Test 3"))
fig7 = my_rm_baseline.mean_diff.plot();

Create a repeated meausures (sequential) Slopeplot.

my_rm_sequential = dabest.load(df, id_col = "ID", paired = "sequential",
                                 idx=("Control 1", "Test 1",
                                          "Test 2", "Test 3"))
fig8 = my_rm_sequential.mean_diff.plot();

---

PermutationTest

def PermutationTest(
    control:array, test:array, # These should be numerical iterables.
    effect_size:str, # Any one of the following are accepted inputs: 'mean_diff', 'median_diff', 'cohens_d', 'hedges_g', or 'cliffs_delta'
    is_paired:str=None, permutation_count:int=5000, # The number of permutations (reshuffles) to perform.
    random_seed:int=12345, # `random_seed` is used to seed the random number generator during bootstrap resampling. This ensures that the generated permutations are replicable.
    ps_adjust:bool=False, kwargs:VAR_KEYWORD
):

A class to compute and report permutation tests.

Notes:

The basic concept of permutation tests is the same as that behind bootstrapping. In an “exact” permutation test, all possible resuffles of the control and test labels are performed, and the proportion of effect sizes that equal or exceed the observed effect size is computed. This is the probability, under the null hypothesis of zero difference between test and control groups, of observing the effect size: the p-value of the Student’s t-test.

Exact permutation tests are impractical: computing the effect sizes for all reshuffles quickly exceeds trivial computational loads. A control group and a test group both with 10 observations each would have a total of \(20!\) or \(2.43 \times {10}^{18}\) reshuffles. Therefore, in practice, “approximate” permutation tests are performed, where a sufficient number of reshuffles are performed (5,000 or 10,000), from which the p-value is computed.

More information can be found here.

Example: permutation test

control = norm.rvs(loc=0, size=30, random_state=12345)
test = norm.rvs(loc=0.5, size=30, random_state=12345)
perm_test = dabest.PermutationTest(control, test, 
                                   effect_size="mean_diff", 
                                   is_paired=None)
perm_test

5000 permutations were taken. The p-value is 0.0758.