import numpy as np
import pandas as pd
import dabest
print("We're using DABEST v{}".format(dabest.__version__))We're using DABEST v2024.03.29Proportion plots
A guide to plot proportion plots with binary data.
As of v2023.02.14, DABEST can be used to generate Cohen’s h and the corresponding proportion plot for binary data. It’s important to note that the code we provide only supports numerical proportion data, where the values are limited to 0 (failure) and 1 (success). This means that the code is not suitable for analyzing proportion data that contains non-numeric values, such as strings like ‘yes’ and ‘no’.
Load libraries
Creating a demo dataset
def create_demo_prop_dataset(seed=9999, N=40):
import numpy as np
import pandas as pd
np.random.seed(9999) # Fix the seed to ensure reproducibility of results.
# Create samples
n = 1
c1 = np.random.binomial(n, 0.2, size=N)
c2 = np.random.binomial(n, 0.2, size=N)
c3 = np.random.binomial(n, 0.8, size=N)
t1 = np.random.binomial(n, 0.6, size=N)
t2 = np.random.binomial(n, 0.2, size=N)
t3 = np.random.binomial(n, 0.3, size=N)
t4 = np.random.binomial(n, 0.4, size=N)
t5 = np.random.binomial(n, 0.5, size=N)
t6 = np.random.binomial(n, 0.6, size=N)
t7 = np.ones(N)
t8 = np.zeros(N)
t9 = np.zeros(N)
# Add a `gender` column for coloring the data.
females = np.repeat('Female', N / 2).tolist()
males = np.repeat('Male', N / 2).tolist()
gender = females + males
# Add an `id` column for paired data plotting.
id_col = pd.Series(range(1, N + 1))
# Combine samples and gender into a DataFrame.
df = pd.DataFrame({'Control 1': c1, 'Test 1': t1,
'Control 2': c2, 'Test 2': t2,
'Control 3': c3, 'Test 3': t3,
'Test 4': t4, 'Test 5': t5, 'Test 6': t6,
'Test 7': t7, 'Test 8': t8, 'Test 9': t9,
'Gender': gender, 'ID': id_col
})
return df
df = create_demo_prop_dataset()
df.head()| Control 1 | Test 1 | Control 2 | Test 2 | Control 3 | Test 3 | Test 4 | Test 5 | Test 6 | Test 7 | Test 8 | Test 9 | Gender | ID | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1.0 | 0.0 | 0.0 | Female | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1.0 | 0.0 | 0.0 | Female | 2 |
| 2 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1.0 | 0.0 | 0.0 | Female | 3 |
| 3 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1.0 | 0.0 | 0.0 | Female | 4 |
| 4 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1.0 | 0.0 | 0.0 | Female | 5 |
Convenient funtion to create a dataset for Unpaired Proportion Plot
In DABEST v2024.3.29, we incorporated feedback from biologists who may not have tables of 0’s and 1’s readily available. As a result, a convenient function to generate a binary dataset based on the specified sample sizes is provided. Users can generate a pandas.DataFrame containing the sample sizes for each element in the groups and the group names (optional if the sample sizes are provided in a dict).
sample_size_1 = {'a':[3, 4], 'b':[2, 5]}
sample_size_2 = [3, 4, 2, 5]
names = ['a', 'b']
sample_df_1 = dabest.prop_dataset(sample_size_1)
sample_df_2 = dabest.prop_dataset(sample_size_2, names)
print(all(sample_df_1 == sample_df_2))
sample_df_1.head()True| a | b | ID | |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 2 |
| 2 | 0 | 1 | 3 |
| 3 | 1 | 1 | 4 |
| 4 | 1 | 1 | 5 |
Loading data
When loading data, you need to set the parameter proportional=True.
two_groups_unpaired = dabest.load(df, idx=("Control 1", "Test 1"), proportional=True)two_groups_unpairedDABEST v2024.03.29
==================
Good afternoon!
The current time is Tue Mar 19 15:37:29 2024.
Effect size(s) with 95% confidence intervals will be computed for:
1. Test 1 minus Control 1
5000 resamples will be used to generate the effect size bootstraps.Effect sizes
To generate a proportion plot, the dabest library features two effect sizes:
- the mean difference (
mean_diff) - Cohen’s h (
[cohens_h](https://acclab.github.io/DABEST-python/API/effsize.html#cohens_h))
These are attributes of the Dabest object.
two_groups_unpaired.mean_diffDABEST v2024.03.29
==================
Good afternoon!
The current time is Tue Mar 19 15:37:30 2024.
The unpaired mean difference between Control 1 and Test 1 is 0.575 [95%CI 0.35, 0.725].
The p-value of the two-sided permutation t-test is 0.0, calculated for legacy purposes only.
5000 bootstrap samples were taken; the confidence interval is bias-corrected and accelerated.
Any p-value reported is the probability of observing theeffect size (or greater),
assuming the null hypothesis of zero difference is true.
For each p-value, 5000 reshuffles of the control and test labels were performed.
To get the results of all valid statistical tests, use `.mean_diff.statistical_tests`Let’s compute the Cohen’s h for our comparison.
two_groups_unpaired.cohens_hDABEST v2024.03.29
==================
Good afternoon!
The current time is Tue Mar 19 15:37:31 2024.
The unpaired Cohen's h between Control 1 and Test 1 is 1.24 [95%CI 0.769, 1.66].
The p-value of the two-sided permutation t-test is 0.0, calculated for legacy purposes only.
5000 bootstrap samples were taken; the confidence interval is bias-corrected and accelerated.
Any p-value reported is the probability of observing theeffect size (or greater),
assuming the null hypothesis of zero difference is true.
For each p-value, 5000 reshuffles of the control and test labels were performed.
To get the results of all valid statistical tests, use `.cohens_h.statistical_tests`Generating proportion plots
To generate a Gardner-Altman estimation plot, simply use the .plot() method.
Each effect size instance has access to the .plot() method, allowing you to quickly create plots for different effect sizes with ease.
two_groups_unpaired.mean_diff.plot();
two_groups_unpaired.cohens_h.plot();
In the bar plot, the white portion represents the proportion of observations in the dataset that do not belong to the category, equivalent to the proportion of 0 in the data. Conversely, the colored portion represents the proportion of observations belonging to the category, equivalent to the proportion of 1 in the data. By default, the value of ‘group_summaries’ is set to “mean_sd,” displaying the mean and ± standard deviation of each group as gapped lines in the plot. The gap represents the mean, while the vertical ends represent the standard deviation. Alternatively, if the value of ‘group_summaries’ is set to “median_quartiles,” the median and 25th and 75th percentiles of each group are plotted. By default, the bootstrap effect sizes are plotted on the right axis.
Instead of a Gardner-Altman plot, you can generate a Cumming estimation plot by setting float_contrast=False in the plot() method. This will plot the bootstrap effect sizes below the raw data.
two_groups_unpaired.mean_diff.plot(float_contrast=False);
You can also modify the width of bars by setting the parameter bar_width in the plot() method.
two_groups_unpaired.mean_diff.plot(bar_width=0.3);
The bar_desat is used to control the amount of desaturation applied to the bar colors. A value of 0.0 means full desaturation (i.e., grayscale), while a value of 1.0 means no desaturation (i.e., full color saturation). The default one is 0.8.
two_groups_unpaired.mean_diff.plot(bar_desat=1.0);
The parameters bar_label and contrast_label can be used to set labels for the y-axis of the bar plot and the contrast plot.
two_groups_unpaired.mean_diff.plot(bar_label="success",contrast_label="difference");
The color of the error bar can be modified by setting err_color.
two_groups_unpaired.mean_diff.plot(err_color="purple");
Generating results
two_groups_unpaired.cohens_h.results| control | test | control_N | test_N | effect_size | is_paired | difference | ci | bca_low | bca_high | ... | pct_high | pct_interval_idx | bootstraps | resamples | random_seed | permutations | pvalue_permutation | permutation_count | permutations_var | proportional_difference | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Control 1 | Test 1 | 40 | 40 | Cohen's h | None | 1.242163 | 95 | 0.769088 | 1.659486 | ... | 1.72357 | (125, 4875) | [1.4827506328621212, 1.0122770907407532, 1.491... | 5000 | 12345 | [-0.25268025514207904, 0.050400851615126196, -... | 0.0 | 5000 | [0.012419871794871796, 0.012612179487179487, 0... | 1.242163 |
1 rows × 22 columns
Producing estimation plots
two_groups_unpaired.mean_diff.plot();
two_groups_unpaired.cohens_h.plot();
The white part in the bar represents the proportion of observations in the dataset that do not belong to the category, which is equivalent to the proportion of 0 in the data. The colored part, on the other hand, represents the proportion of observations that belong to the category, which is equivalent to the proportion of 1 in the data. By default, the value of “group_summaries” is set to “mean_sd”. This means that the error bars in the plot display the mean and ± standard deviation of each group as gapped lines. The gap represents the mean, while the vertical ends represent the standard deviation. Alternatively, if the value of “group_summaries” is set to “median_quartiles”, the median and 25th and 75th percentiles of each group are plotted instead. By default, the bootstrap effect sizes is plotted on the right axis.
Instead of a Gardner-Altman plot, you can generate a Cumming estimation plot by setting float_contrast=False in the plot() method. This will plot the bootstrap effect sizes below the raw data.
two_groups_unpaired.mean_diff.plot(float_contrast=False);
Generating Sankey plots for paired proportions and repeated-measures proportions
For the paired version of the proportion plot, we adopt the style of a Sankey Diagram. The width of each bar in each xtick represents the proportion of the corresponding label in the group, and the strip denotes the paired relationship for each observation.
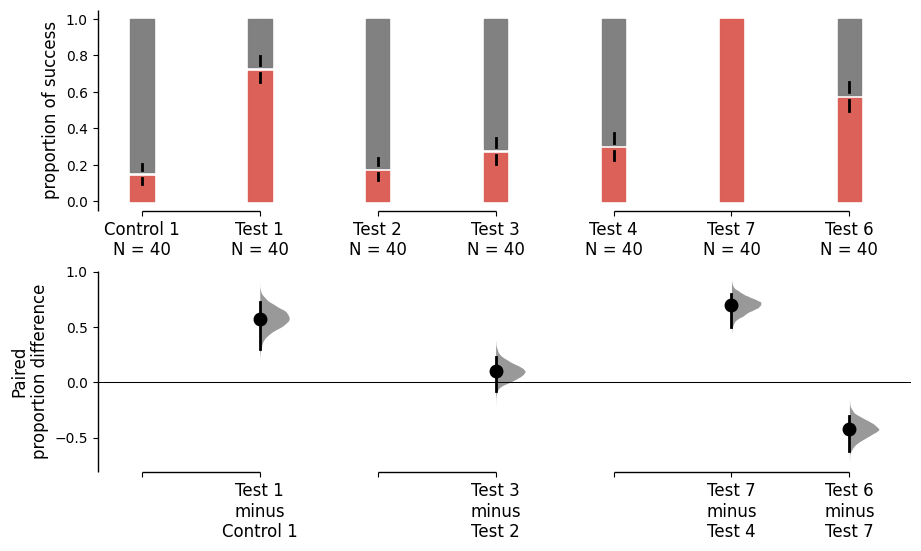
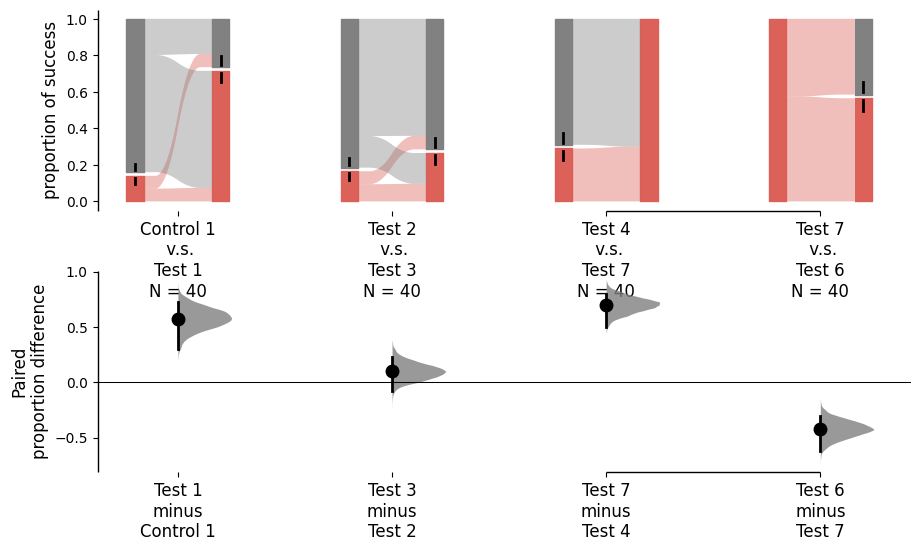
Starting from v2024.3.29, the paired version of the proportion plot receives a major upgrade. We introduce the sankey and flow parameters to control the plot. By default, both sankey and flow are set to True to cater the needs of repeated measures. When sankey is set to False, DABEST will generate a bar plot with a similar aesthetic to the paired proportion plot. When flow is set to False, each group of comparsion forms a Sankey diagram that does not connect to other groups of comparison.
Similar to the unpaired version, the .plot() method is used to produce a Gardner-Altman estimation plot, the only difference is that the is_paired parameter is set to either baseline or sequential when loading data.
two_groups_baseline = dabest.load(df, idx=("Control 1", "Test 1"),
proportional=True, paired="baseline", id_col="ID")
two_groups_baseline.mean_diff.plot();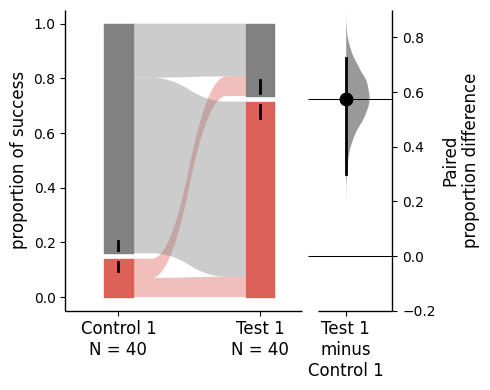
The Sankey plots for paired proportions also supports the float_contrast parameter, which can be set to False to produce a Cumming estimation plot.
two_groups_baseline.mean_diff.plot(float_contrast=False);
The upper part (grey section) of the bar represents the proportion of observations in the dataset that do not belong to the category, equivalent to the proportion of 0 in the data. The lower part, conversely, represents the proportion of observations that belong to the category, synonymous with success, equivalent to the proportion of 1 in the data.
Repeated measures are also supported in the Sankey plots for paired proportions. By adjusting the is_paired parameter, two types of plot can be generated.
By default, the raw data plot (upper part) in both baseline and sequential repeated measures remains the same; the only difference is the lower part. For detailed information about repeated measures, please refer to repeated measures .
multi_group_baseline = dabest.load(df, idx=((("Control 1", "Test 1","Test 2", "Test 3"),
("Test 4", "Test 5", "Test 6"))),
proportional=True, paired="baseline", id_col="ID")
multi_group_baseline.mean_diff.plot();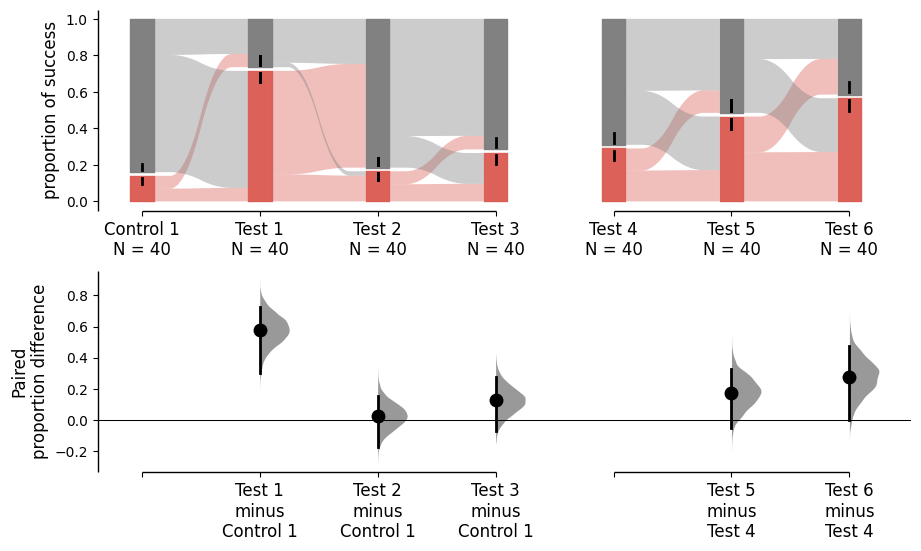
multi_group_sequential = dabest.load(df, idx=((("Control 1", "Test 1","Test 2", "Test 3"),
("Test 4", "Test 5", "Test 6"))),
proportional=True, paired="sequential", id_col="ID")
multi_group_sequential.mean_diff.plot();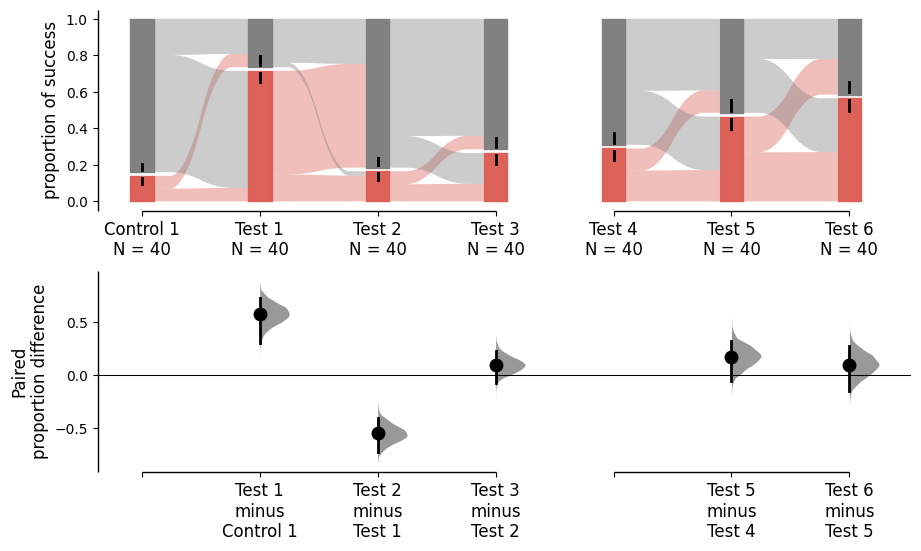
If you want to specify the order of the groups, you can use the idx parameter in the .load() method.
To compare all groups together, you can include all the groups in the idx parameter of the load() method without using subbrackets.”
multi_group_baseline_specify = dabest.load(df, idx=(("Control 1", "Test 1","Test 2", "Test 3",
"Test 4", "Test 5", "Test 6")),
proportional=True, paired="baseline", id_col="ID")
multi_group_baseline_specify.mean_diff.plot();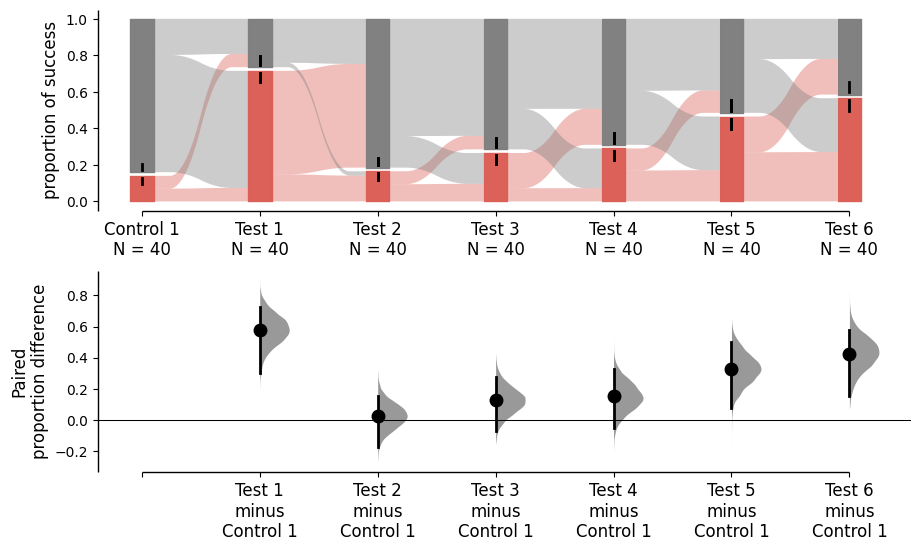
By changing the sankey and flow parameters, you can generate different types of Sankey plots for paired proportions.
separate_control = dabest.load(df, idx=((("Control 1", "Test 1"),
("Test 2", "Test 3"),
("Test 4", "Test 7", "Test 6"))),
proportional=True, paired="sequential", id_col="ID")
separate_control.mean_diff.plot();
separate_control.mean_diff.plot(sankey_kwargs={'sankey':False});
separate_control.mean_diff.plot(sankey_kwargs={'flow':False});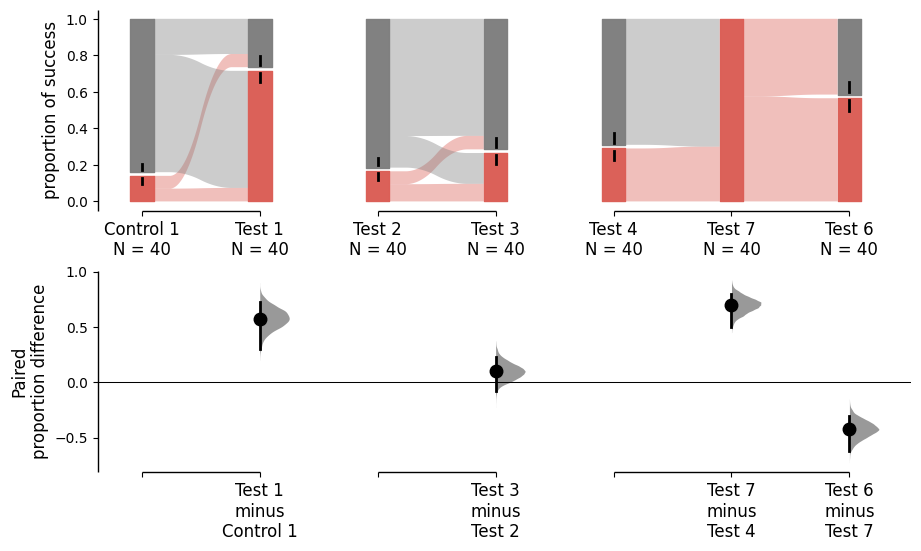
Several exclusive parameters can be provided to the plot() method to customize the Sankey plots for paired proportions. By modifying the sankey_kwargs parameter, you can customize the Sankey plot. The following parameters are supported:
- width: The width of each Sankey bar. Default is 0.5.
- align: The alignment of each Sankey bar. Default is “center”.
- alpha: The transparency of each Sankey bar. Default is 0.4.
- bar_width: The width of each bar on the side in the plot. Default is 0.1.
two_groups_baseline.mean_diff.plot(sankey_kwargs = {"alpha": 0.2});